
Basics of 3D-Vector Graphics
Copyright © by V. Miszalok, last update: 2011-04-29

Let me know
what you think
| Home | Index of Lectures | Next >> | PDF Version of Page |
 |
Basics of 3D-Vector GraphicsCopyright © by V. Miszalok, last update: 2011-04-29 |
 Let me know what you think |
|
| Objectives |
|
Understanding 1) left- and right hand coordinate systems, |
| Summary |
|
3D just needs a third shift dz and a third scale factor zoomx. |
|
But there are two new rotations around the x- and the y-axes. (2D just has one type of rotation around the Z-axis.) |
Each vertex can be regarded as a vector having its tail at (0,0,0). |
|
Vector addition vi + vi+1: Set the tail of vi+1 to the head of vi. You obtain a new vector from the tail of vi to the head of of vi+1. |
|
Vector subtract vi - vi+1: new vector from the head of vi to he head of vi+1. |
|
Vector scalar product vi * vi+1: = cosinus(enclosed angle), when the length of both vi and vi+1 is 1. |
|
Vector cross product vi x vi+1: new vector perpendicular to both vi and vi+1 (= normal vector). |
|
At each vertex one to many normals can be computed depending on the no. of touching triangles. |
|
The final normal vector attached to a vertex is the mean of all its triangle normals. |
Spricht man von 3D, ist so gut wie immer 3D-Vektorgraphik gemeint. 3D-Rastergraphik gibt es nur in exotischen Anwendungen in der Medizin, Materialforschung und Geologie, aber nicht bei Games und Unterhaltung. Auf dem PC des Normalbürgers existiert nur 2D-Rastergraphik. Den Vorlesungstitel "3D-Vektorgraphik" könnte man folglich kürzer fassen: "3D-Graphik" würde ausreichen.
Jede Polygonecke bekommt zusätzlich zu seiner x- und y-Koordinate noch eine z-Koordinate. In diesem Sinne war jede 2D-Vektorgraphik schon immer eine 3D-Vektorgraphik, nur hatten alle z-Koordinaten den Wert 0.0f und weil diese immer Null waren, waren sie nicht erwähnt worden.
Beispiel für die Erweiterung von Scroll, Zoom und Rot von 2D nach 3D:
double arcus = alpha * 2.0 * Math.PI / 360.0;
float cosinus = (float)Math.Cos( arcus );
float sinus = (float)Math.Sin( arcus );
for ( i=0; i<n; i++ )
{ p[i].X += dx;
p[i].Y += dy;
p[i].Z += dz; //new dimension
p[i].X *= zoomx;
p[i].Y *= zoomy;
p[i].Z *= zoomz; //new dimension
float help = p[i].X * cosinus - p[i].Y * sinus;
p[i].Y = p[i].X * sinus + p[i].Y * cosinus;
p[i].X = help; //Rot-operation around the z-axis doesn't change
}
Scroll und Zoom bekommen in 3D je eine neue z-Zeile, die 2D-Rotation bleibt identisch in 3D erhalten ohne neue z-Zeile. Begründung: Die Drehung in der x,y-Ebene ist eine Drehung um eine Achse senkrecht zur Ebene = z-Achse. Bei einer solchen Drehung behalten alle Vertices ihre z-Koordinaten, nur ihre x- und y- Koordinaten ändern sich.
| Man kann die z-Achse entweder vor oder hinter die x,y-Ebene stellen. Dadurch entstehen zwei verschiedene Koordinatensysteme, was viel Verwirrung stiftet. Default zeigt bei DirectX und OpenGL die z-Achse hinter die x,y-Ebene des Displays = Left-Hand Cartesian Coordinate System = x-Achse von links nach rechts, y-Achse von unten nach oben, z-Achse von vorn nach hinten. Mehr Information: 3-D Coordinate Systems | 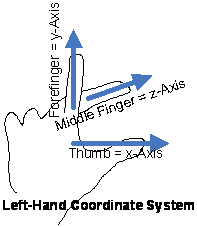 |
| Es gibt in 3D neue, in 2D unbekannte Drehungen, nämlich die um die x-Achse und um die y-Achse. 3D kennt folglich nicht nur eine Art von Drehung sondern drei Arten mit jeweils eigenem Winkel, die nach Seemannsart benannt sind: Roll = Rollwinkel = Drehwinkel um die x-Achse (in Fahrtrichtung) Pitch = Neigungswinkel = Drehwinkel um die y-Achse Yaw = Gierwinkel = Drehwinkel um die z-Achse Vorsicht: Rätselhafterweise nennt die DirectX-Funktion RotationYawPitchRoll die 3 Drehungen in der Reihenfolge z, y, x und erwartet die Winkelparameter auch so. siehe: http://msdn.microsoft.com/en-us/library/bb281744.aspx In 2D gibt es nur Yaw-Winkel, die man meist alpha nennt. |
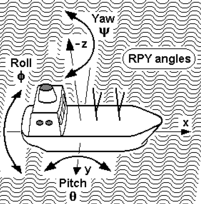 siehe: de.wikipedia.org/wiki/Roll-Nick-Gier-Winkel |
Die Begriffe Vertex und Vektor scheinen zunächst identische Bedeutung zu haben.
Beide bezeichnen eine Datenstruktur vom Typ
Anschauliche Interpretation von Vertex ist ein Raumpunkt ähnlich einem Stern im Weltraum. Ein Array von Vertices stellt man sich folglich als eine Punktwolke oder eine Art Sternenwolke vor.
Vorteil: einfach. Nachteil: Man hat keinen Zugang zur Vektorrechnung.
Anschauliche Interpretation von Vektor ist ein Pfeil vom Ursprung des Koordinatensystems (0,0,0), der an einer Stelle (x,y,z) seine Spitze hat. Ein Array von Vektoren stellt man sich folglich als ein Bündel von Pfeilen vor, die strahlenförmig von (0,0,0) nach außen zeigen. Jeder Pfeil besitzt einen Raumwinkel und eine Länge.
Vorteil: Vektoren kann man addieren, subtrahieren und multiplizieren. Nachteil: komplizierter als Vertex.
1) Vektoraddition : v0 + v1 = { v0.X+v1.X, v0.Y+v1.Y, v0.Z+v1.Z } setzt v1 an die Spitze von v0 und zeigt dann vom Fußpunkt von v0 an die Spitze von v1.
2) Vektorsubtraktion: v1 - v0 = { v1.X-v0.X, v1.Y-v0.Y, v1.Z-v0.Z } ist der Vektor von der Spitze von v0 zur Spitze von v1.
3) Skalarprodukt : v0 * v1 = v0.X*v1.X +v0.Y*v1.Y +v0.Z*v1.Z = cos(alpha) ist der Cosinus des Winkels zwischen v0 und v1,
4) Kreuzprodukt : ist ein Vektor, der senkrecht steht auf der Ebene, die von v0 und v1 aufgespannt wird.
v0 x v1 = { v0.Y*v1.Z - v0.Z*v1.Y,
v0.Z*v1.X - v0.X*v1.Z,
v0.X*v1.Y - v0.Y*v1.X }
5) Betrag = Länge von v : Länge = Math.Sqrt( v.X2 + v.Y2 + v.Z2 ).
Anwendungen:
Für 1) gibt es nur selten eine Verwendung in der 3D-Graphik (wohl aber in der Physik).
Mit 2) berechnet man die Verbindungsvektoren zwischen den Vertices.
Mit 3) berechnet man den Auftreffwinkel des gerichteten Lichts auf eine Fläche = Face = meistens Dreieck.
Mit 4) berechnet man die Normale einer Fläche = Face = meistens Dreieck.
Mit 5) berechnet man die Länge und wenn die Länge eines Vektors keine Rolle spielen soll, kappt man diese auf 1.0 = normierter Vektor
Zusammenfassung: Benutzen Sie zunächst die einfache Vertex-Denkweise und wenn Sie Winkel, Normale und Normierung brauchen, wechseln Sie zur komplizierteren Vektor-Denkweise.
2D-Flächen haben nur Vorderseiten, in 3D muss man sich auch um Rückseite und Orientierung kümmern.
3D-Flächen = Faces benötigen deshalb in der Regel eine Normale = "Face Normal" = senkrechter Lotvektor auf die Fläche. Richtung zur Außenwelt.
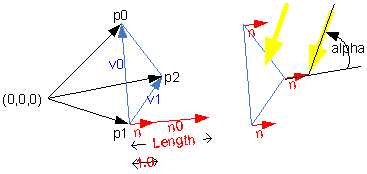 | siehe: Cross Product Applet www.phy.syr.edu/courses/java-suite/crosspro.html |
Die Normale bestimmt, wo Vorder- und wo Rückseite ist und in welchem Winkel alpha Face zum Licht steht. Aus dem Skalarprodukt normierte Normale mal normiertem Lichtvektor erhält man cos(alpha), was die Helligkeit bestimmt. Face ist am hellsten, wenn das Licht koaxial zur Normalen auftrifft. Beispiele:
| alpha [Grad] | 0 | 30 | 45 | 60 | 90 | 120 | 180 | 360 |
| cos(alpha) | 1.0 | 0.87 | 0.71 | 0.5 | 0.0 | -0.5 | -1.0 | 1.0 |
| Helligkeit | 100% | 87% | 71% | 50% | 0% | 0% | 0% | 100% |
Bei Faces, die keine Normale haben, behilft man sich mit einer Konvention: Man stellt sich auf den zweiten Vertex p[1] und richtet den linken Daumen nach dem ersten Vertex p[0] und den Zeigefinger nach dem dritten Vertex p[2]. Das Face bekommt seine Normale auf die Seite auf die jetzt der angewinkelte Mittelfinger zeigt.
In DirectX3D und in OpenGL gibt man nicht jedem Face, sondern jedem Vertex eine Normale = "Vertex Normal". Ein Dreieck besitzt also drei parallele "Vertex Normals", was redundant und widersinnig ist bei einem einzelnen Dreieck.
Wenn jedoch drei oder mehr Dreiecke wie z.B. an einer Pyramidenspitze zusammenstoßen, dann kann man die am Punkt versammelten Normalen zu einer Durchschnittsnormalen mitteln, die die Ecke sehr gut repräsentiert.
Der Vorteil zeigt sich bei TriangleStrips an Kanten, wo Dreiecke scharfkantig zusammenstoßen. Anstatt des scharfen Farbsprungs bei schräger Beleuchtung → Flat Shading ergeben die gemittelten Normalen einen sanften Übergang → Gouraud-Shading.


Shading-Verfahren = Vortäuschen einer Tiefe durch Licht- und Schatteneffekte.
Gouraud-Shading von 1971 benannt nach dem Studenten Henri Gouraud (sprich: Guro).
Ähnlich: Phong-Shading, Metal Shading
| top of page: |