
Textbook on Image Filters
Chapter 9 - The Histogram
Copyright: V. Miszalok
Last Modified:

Copyright: V. Miszalok
Last Modified:
The histogram H of a gray value image is an integer-array of lenght 256, where H[g] contains the no. of pixels carrying the gray value g.
H[0] contains the no. of zeros, H[1] the no. of ones et cetera.
The sum of all histogram values must give the total no of pixels !
Pseudo-code of the check whether a histogram H fits to an image I[width*height]:
sum = 0; for (int i=0; i < 256; i++ ) sum += H[i];
if ( sum != width*height ) -> Histogram H doesn't fit to image I !
Black-and-white images have one, true color images have three histograms.
A histograms shows the statistical distribution of brightness values of a picture.
It informs about basic image properties such as exposure, contrast, color proportions.
Code to compute the histogram int H[256] of an image Byte I[ySize][xSize],
H must be pre-filled with 0.
Slow code:
for ( y=0; y < ySize; y++ )
for ( x=0; x < xSize; x++ )
H[I[y][x]]++;
Fast code:
int* pointer = I;
for ( i=0; i < xSize*ySize; i++ ) H[*(pointer+i)]++;
Very fast code:
for ( int* pointer = I; pointer < I + xSize*ySize; ) H[*pointer++]++;
Mini-Sample: The histogram H[10] of mini-image I[4][5]
01020
I[4][5]= 27891 Solution: H = [ 5, 4, 3, 2, 0, 1, 1, 2, 1, 1 ]
06571 Proof: The sum of the histogram must be ySize*xSize = 4*5 = 20.
13230
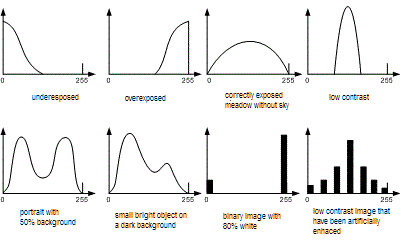
As a rule histograms are plotted in form of a bar chart with:
gray values extending from 0 to 255 on the horizontal axis and
normalized frequencies of gray values on the vertical axis.
Professional video cameras monitor three (RGB) histograms online on the screen, which makes it possible for the cameraman to control exposure, aperture, image section etc.
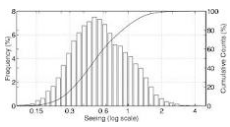
The cumulative histogram is the image's accumulated normalized histogram in which the vertical axis gives not just the counts for a single gray, but rather gives the counts for that gray plus all left-side values:
for (i=0; i < gray; i++) CumulativeHistogram[gray] += Histogram[i];
Cumulative histograms can give sense to visualize the result of contrast stretching operations.
Binarisation by Thresholding is an important first step of pattern recognition.
It requires a fixed threshold to separate foreground from background.
A histogram with two peaks is ideal to determine the threshold in the mid of the valley between the peaks.
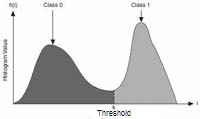
Binarisation of images with a two peak histogram:
Slow code:
for ( y=0; y < ySize; y++ )
for ( x=0; x < xSize; x++ )
if ( I[y][x]] < threshold ) I[y][x] = 0; else I[y][x] = 255;
Fast code:
int* pointer = I;
for ( i=0; i < xSize*ySize; i++, pointer++ ) if ( *pointer < threshold ) *pointer = 0; else *pointer = 255;
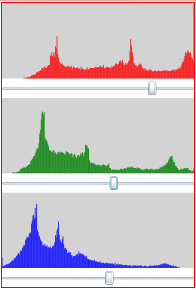
WriteableBitmap img0, img1; //input+output images
Int32 xSize, ySize; //image width+height
Int32[] Histogram = new Int32[256];
Brush brush = new SolidColorBrush( Colors.Black );
Int32 threshold = 255;
Int32[xSize*ySize] RGB; //intermediary array for (r+g+b)/3
Canvas HistogramCanvas: //area to draw lines
private void ComputeColorHistogram()
{ for ( int gray=0; gray < 256; gray++ ) Histogram[gray] = 0; //clear
for ( int i=0; i < xSize*ySize; i++ ) //for all Int32-pixels
{ Int32 r, g ,b, argb = img0.Pixels[i]; //local variables
r = (argb & 0xff0000) >> 16; //Cut out red and shift it down.
g = (argb & 0x00ff00) >> 8; //Cut out green and shift it down.
b = argb & 0x0000ff; //Cut out blue.
RGB[i] = (r + g + b) / 3; //gray = mean of r+g+b
Histogram[RGB[i]]++; //Increment the histogram bar no. RGB[i].
}
//Normalisation: Scale the tallest bar of the histogram to height = 100.
Int32 max = 0;
for ( int gray=0; gray < 256; gray++ ) //maximum finder
if ( Histogram[gray] > max ) max = Histogram[gray];
float factor = 100f / max; //normalisation factor
for ( int gray=0; gray < 256; gray++ )
Histogram[gray] = Convert.ToInt32(Histogram[gray] * factor);
HistogramCanvas.Children.Clear(); //throw away any former graphics.
//Draw 256 vertical bars on the canvas.
for ( int gray=0; gray < 256; gray++ )
{ Line line = new Line(); line.X1 = line.X2 = gray;
line.Y1 = 100; line.Y2 = 100 - Histogram[gray];
line.Stroke = brush; line.StrokeThickness = 1;
HistogramCanvas.Children.Add( line );
}
}
img0[i] are 32-bit integers carrying 4 bytes.0xff. The color bytes must be cut out by 3 bit-masks 0x00ff0000, 0x0000ff00, 0x000000ff.RGB[i] = (r + g + b) / 3; averages the three colors to a single brightness value,Histogram[RGB[i]]++; sums up.WriteableBitmap img0, img1; //input+output images
Int32 xSize, ySize; //image width+height
Int32[,] Histogram = new Int32[3,256]; //3 histograms
Brush[] brush = { new SolidColorBrush( Colors.Red ), //3 brushes
new SolidColorBrush( Colors.Green ),
new SolidColorBrush( Colors.Blue ) };
Int32[] threshold = { 255, 255, 255 }; //3 thresholds
Int32[] R; //intermediary array for red
Int32[] G; //intermediary array for green
Int32[] B; //intermediary array for blue
Canvas[] canvas = new Canvas[3]; //3 areas to draw lines
private void ComputeColorHistogram()
{ for ( int color=0; color < 3; color++ )
for ( int gray=0; gray < 256; gray++ ) Histogram[color,gray] = 0; //clear
for ( int i=0; i < xSize*ySize; i++ ) //for all Int32-pixels
{ Int32 argb = img0.Pixels[i]; //local variables
R[i] = (argb & 0xff0000) >> 16; //Cut out red and shift it down.
G[i] = (argb & 0x00ff00) >> 8; //Cut out green and shift it down.
B[i] = argb & 0x0000ff; //Cut out blue.
Histogram[0,R[i]]++; //Increment the histogram bar no. R[i].
Histogram[1,G[i]]++; //Increment the histogram bar no. G[i].
Histogram[2,B[i]]++; //Increment the histogram bar no. B[i].
}
//Scale the tallest bar of the histogram to height = 100.
Int32 max = 0;
for ( int color=0; color < 3; color++ )
for ( int gray=0; gray < 256; gray++ )
if ( Histogram[color,gray] > max ) max = Histogram[color,gray];
float factor = 100f / max;
for ( int color=0; color < 3; color++ )
{ for ( int gray=0; gray < 256; gray++ )
Histogram[color,gray] = Convert.ToInt32(Histogram[color,gray] * factor);
canvas[color].Children.Clear(); //Throw away any former canvas content.
//Draw 256 vertical bars on the canvas.
for ( int gray=0; gray < 256; gray++ )
{ Line line = new Line(); line.X1 = line.X2 = gray;
line.Y1 = 100; line.Y2 = 100 - Histogram[color,gray];
line.Stroke = brush[color]; line.StrokeThickness = 1;
canvas[color].Children.Add( line );
}
}
}
img0[i] are 32-bit integers carrying 4 bytes.0xff. The color bytes must be cut out by 3 bit-masks 0x00ff0000, 0x0000ff00, 0x000000ff.R[i], G[i], B[i] store the color planes for further use in thresholding,Histogram[0,R[i]]++; and sums up the first (red) histogram.******************************************************************************
Q: What is a histogram H ? Purpose ?
A: An array H: int[256], where element H[g] contains the no. of pixels carrying the gray value g.
It shows the statistical distribution of brightness values of a picture and basic image properties such as exposure, contrast, color proportions.
******************************************************************************
Q: Pseudo-code of a histogram H[256] of a black-and-white image I[width*height] ?
A: for (int i=0; i < width*height; i++) H[I[i]]++;
******************************************************************************
Q: Pseudo-code of 3 histograms Red[256], Green[256], Blue[256] of a color image I[width*height] ?
A:
for (int i=0; i < width*height; i++)
{ Red [red byte of I[i]]++;
Green[green byte of I[i]]++;
Blue [blue byte of I[i]]++;
}
******************************************************************************
Q: What is the histogram H[10] of the following 5x4-image ? Check the result !
0 1 0 2 0
2 7 8 9 1
0 6 5 7 1
1 3 2 3 0
A: H = [ 5, 4, 3, 2, 0, 1, 1, 2, 1, 1 ]
Check: 5+4+3+2+0+1+1+2+1+1 = 20 = 5*4
******************************************************************************
Q: Samples of frequent and famous histograms ?
A:

******************************************************************************
Q: What is histogram normalisation ?
A: Linear upset of the (normally huge) maximal value of the array to a fixed value e.g. 100.
******************************************************************************
Q: How to compute a cumulative histogram ?
A: for (i=0; i < gray; i++) CumulativeHistogram[gray] += Histogram[i];
******************************************************************************
Q: What is binarisation ? Pseudo-code of thresholding ?
A: Reducing a black-and-white image to just two gray values e.g. 0 and 255.
If ( pixel < threshold ) pixel = black; else pixel = white;
******************************************************************************