Home Content «Highpass_Filters Histogram»

Textbook on Image Filters
Chapter 8 - Convolution
Copyright: V. Miszalok
Last Modified:
Home Content «Highpass_Filters Histogram»

Copyright: V. Miszalok
Last Modified:
See:Interactive Java Tutorial of the Florida States University
The filters presented in the previous chapters of this textbook can be divided into 3 types.
Type 1 filters and the linear part of the type 3 filters base on a common filter algorithm called discrete 2D spatial convolution or shortly convolution.
Convolution is a powerful instrument to improve images in many ways:
Such different imaging tasks can be carried out by one convolution algorithm which always follows these 3 steps:
0 and 255.A problem with image convolution is the enormous number of multiplications and additions that need to be performed, often resulting in unacceptably long execution times.
Solution: Modern graphics cards contain special hardware processors that boost convolution.
 |
Convolution unifies all sorts linear filtering: lowpass, highpass, bandpass.
Advantages:
Disadvantages:
|
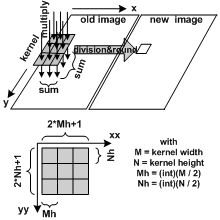
The algorithm contains 4 for loops:
for loops iterate over the 2D input image img0.for loops iterate over the small 2D kernel matrix.img0.divisor >= 1.Byte and written into the output image img1.mh columns and nh rows of img1 remain undefined.Here is the pseudocode of convolution:
const int m; //no of kernel columns must be uneven >= 3
const int m; //no of kernel rows must be uneven >= 3
const int mh = (m-1)/2, nh = (n-1)/2; //half wings lengths
float sum; const float divisor = ?.???; //divisor = sum of all kernel values (mostly)
for ( int y=nh; y < img0.Height-nh; y++ )
for ( int x=mh; x < img0.Width-mh; x++ )
{ sum = 0.0f;
for ( int yy=-nh; yy <= nh; yy++ )
for ( int xx=-mh; xx <= mh; xx++ )
sum += img0[y+yy,x+xx] * kernel[yy+nh,xx+mh];
img1[y,x] = Convert.ToByte( sum / divisor );
}
 | Result: blurring |
 | Result: nearly no blurring |
 | Result: Sharpening highpass. Explanation: Flat areas remain untouched whereas any difference between center and periphery doubles. |
 | Result: Edge detection highpass. Explanation: Nearly everywhere the colors sum up to 0. Colors just survive at sharp edges. |
 | Result: Same as Average 3x3. Explanation: Inside a kernel only relative differences count. |
WriteableBitmap img0, imgOut; //input and output images with 32-bit-ARGB-pixels
int xSize, ySize; //image width and height
float[,] kernel[n,m]; // m and n are uneven numbers e.g. 3, 5, 7, 9, 11, ...
//R0, G0, B0: intermediary 2D-arrays each containing a color plane of img0
Byte[,] R0[ySize,xSize], G0[ySize,xSize], B0[ySize,xSize];
private void Convolution()
{ int m = kernel.GetLength(0); //no of kernel columns
int n = kernel.GetLength(1); //no of kernel rows
int mh = (m-1) / 2; //horizontal half wing length
int nh = (n-1) / 2; //vertical half wing length
int i, x, y, xx, yy, xxx, yyy, R, G, B;
float weight, sumR, sumG, sumB, divisor=0;
//Add all kernel values to obtain a divisor
for ( yy=0; yy < n; yy++ )
for ( xx=0; xx < m; xx++ ) divisor += kernel[yy,xx];
if ( divisor < 1f ) divisor = 1f; //divisor must be >= 1
//Preset all 32-bit-ARGB-pixels with A = ff and RGB = 000000
for ( i=0; i < xSize*ySize; i++ ) unchecked { imgOut.Pixels[i] = (Int32)0xff000000; }
//Here begins the convolution
for ( y=nh; y < ySize-nh; y++ )
{ i = y*xSize + mh; //linear index of the first pixel in row y
for ( x=mh; x < xSize-mh; x++, i++ ) //increment x and i
{ sumR = sumG = sumB = 0;
for ( yy=0; yy < n; yy++ )
{ yyy = y+yy-nh;
for ( xx=0; xx < m; xx++ )
{ xxx = x+xx-mh;
weight = kernel[yy,xx];
sumR += R0[yyy,xxx] * weight;
sumG += G0[yyy,xxx] * weight;
sumB += B0[yyy,xxx] * weight;
}
}
//Divide, convert to positive integer and clip to maximal 255
R = Math.Min(255, Convert.ToInt32(Math.Abs(sumR/divisor)));
G = Math.Min(255, Convert.ToInt32(Math.Abs(sumG/divisor)));
B = Math.Min(255, Convert.ToInt32(Math.Abs(sumB/divisor)));
//Shift the color bytes to their 32-bit-ARGB positions
imgOut.Pixels[i] += R << 16 | G << 8 | B;
}
}
}******************************************************************************
Q: What is linear Filter ? What is the basic difference to non-linear Filters ? Samples for both ?
A: A linear filter performs a convolution. Non-linear filters don't.
Linear samples: Average, Fog, Gaussian
Non-linear sample: Median
******************************************************************************
Q: What is a convolution ? Short description of the algorithm ?
A: Convolution is a mathematical operation on an image and a kernel, producing a modified version of the original image.
******************************************************************************
Q: What is a kernel ? Kernels of 3x3 Average-, Fog-, horizontal Laplace-filters ?
A: A matrix of figures with an uneven no of columns m >= 3 and an uneven no of rows n >= 3 used for convolution.
1 1 1 1 1 1 -1 0 1
Average = 1 1 1; Fog = 1 -5 1; Horiz. Laplace = -2 0 2
1 1 1 1 1 1 -1 0 1
******************************************************************************
Q: Pseudocode of the convolution img0 -> img1 ?
A:
for ( all lines y of img0 )
for ( all columns x of img0 )
{ sum = 0.0f;
for ( all lines yy of the kernel )
for ( all columns xx of the kernel )
sum += img0[y+yy,x+xx] * kernel[yy,xx];
img1[y,x] = ConvertToColor( sum / divisor );
}
******************************************************************************