

| Home | Index F&A | << Prev | Next >> | Print Version of this Page |
 |
Let me know what you think |
 |
Fragen und Antworten: Computer VisionCopyright © by V. Miszalok, last update: 2011-01-27 |
Solche Fragen und Antworten sind niemals 100% fehlerfrei. Bitte: Wenn Sie einen Fehler finden, und sei es auch nur ein Tippfehler, bitte formlose Mail an prof@miszalok.de
Zum Drucken: FragenUndAntworten.pdf
Zum Drucken: FragenOhneAntworten.pdf
F: Gegeben sei ein Pixel(x,y) in einer Spalte x und einer Zeile y.
Schreiben Sie die Koordinaten seiner 8 Nachbarn links-oben, oben, rechts-oben, rechts, usw.
|
A: |
|
F: Erklären Sie die Vor- und Nachteile der 4er- und der 8er-Nachbarschaft.
A: 4er Vort.: Vorder-Hintergrundvertauschungen möglich;
4er Nacht.: fehlender Zusammenhang von schrägen Linien widerspricht der menschlichen Anschauung.
Ausweg: alle schrägen Linien doppelt dick machen.
8er: Vort.: entspricht der menschlichen Anschauung.
8er Nacht.: Widerspruch wenn zwei Einsen über Eck zusammenhängen, können unmöglich die beiden Nullen ebenfalls zusammenhängen.
Ausweg durch Hilfskonstruktion: Wenn im Vordergrund 8er Nachbarschaft gilt, dann gilt automatisch im Hintergrund nur 4er Nachbarschaft.
F: Gegeben sei ein 4-zeiliges Binärbild
101000
B = 100100
100010
100001
Wie viele Gebiete gibt es im Vordergrund 1 und wie viele im Hintergrund 0 bei 4er Nachbarschaft ?
Wie viele Gebiete gibt es im Vordergrund 1 und wie viele im Hintergrund 0 bei 8er Nachbarschaft ?
A:
4er: VG: 5 Gebiete, HG: 2 Gebiete
8er: VG: 2 Gebiete, HG: 1 Gebiet
F: Wie lang ist der Weg von (x0,y0) nach (x1,y1) in der euklidischen Metrik (Pythagoras) und in der Raster-Metrik (City-Block-Distance) ?
A: Euklid: Weglänge = Wurzel( (x1-x0)*(x1-x0) + (y1-y0)*(y1-y0) );
Raster: Weglänge = Betrag(x1-x0) + Betrag(y1-y0);
F: Durch welche Zellen ist ein 3D-Raster aufgebaut ? Was sagt die Berandungsrelation ? Beispiele ?
A: 3D-Cells=Voxels, 2D-Cells=Pixels, 1D-Cells=Cracks, 0D-Cells=Points.
BR: Eine Zelle der Dimension n wird niemals von anderen Zellen der Dimension n berandet, sondern nur von Zellen niederer Dimension n-1, n-2 etc.
Beispiele: Ein Voxel wird berandet von 6 Pixeln, 12 Cracks und 8 Points. Ein Pixel wird berandet durch 4 Cracks und 4 Points. Ein Crack wird berandet durch 2 Points.
F: Gegeben sei ein Binärbild C2. Was versteht man unter C1V-, C1H- und C0-Matrix ?
A: Die C1V-Matrix kodiert die vertikalen Cracks zwischen einem Vordergrund- und einem Hintergrundpixel (linke und rechte vertikale Seitenwände der Begrenzung).
C1H kodiert die horizontalen Cracks zwischen einem Vordergrund- und einem Hintergrundpixel (horizontale Decken und Böden der Begrenzung).
C0 kodiert die Endpunkte aller Cracks, die in C1V und C1H vorkommen.
Die C1V- und die C0-Matrix sind eine Spalte breiter als die C2-Matrix,
die C1H- und die C0-Matrix sind eine Zeile höher als die C2-Matrix.
F: Gegeben sei ein 4x3 Grauwertbild und die Schwelle s = 2.
Gesucht: C2-, C1V-, C1H- und C0-Matrix.
1030
Bild = 1456
1300
A:
0010 00110 0010 00110
C2 = 0111; C1V = 01001; C1H = 0101; C0 = 01111;
0100 01100 0011 01111
0100 01100F: Was ist der Freeman-Code ?
| A: | 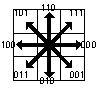 | Freeman- = Chain- = Ketten-Code populär seit 1970 kodiert Pixelketten durch x- und y-Koordinate des Startpixels plus eine Kette von 8 Richtungen zu den Nachfolgepixeln. Richtungscode: von 0 Grad im Uhrzeigersinn in 45 Grad-Schritten: 000,001,010,011,100,101,110,111. |
F: Warum ist der Freeman-Code ungeeignet zur Kodierung von Gebietsbegrenzungen ? Probleme ?
A: Die Berandungsrelation verlangt, dass Pixel niemals durch Pixel, sondern nur durch Cracks und Points berandet werden.
Problem 1: Unklar, ob die Kette am Rand des Vordergrundes oder am Rand des Hintergrundes verlaufen soll → Widerspruch zwischen innerer und äußerer Berandung.
Problem 2: Unklar bei kleinen Gebieten: Welche Kette begrenzt ein einzelnes Pixel ?
F: Der Chain-Code und seine Eigenschaften ?
| A: | 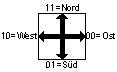 | Moderner Code für Gebietsbegrenzungen kodiert, ausgehend von einer 0-Zelle (x0,y0) die Begrenzung als Kette gerichteter Cracks 00=Ost, 01=Süd, 10=West, 11=Nord. Berandungsrelation wird beachtet. Eigenschaft 1: Anzahl der Südcracks = Anzahl der Nordcracks Eigenschaft 2: Anzahl der Ostcracks = Anzahl der Westcracks Eigenschaft 3: Umfang des Gebiets = Anzahl der Cracks Konvention 1: Startpixel immer am ersten, obersten Übergang von Hintergrund auf Vordergrund. Konvention 2: Startcrack ist immer Süd, d.h. Umlaufrichtung immer so, dass Vordergrund linkerhand und Hintergrund rechterhand. |
F: Verfolgungsalgorithmus bei 4er Nachbarschaft in Form eines Pseudocodes ?
A: if ( Pixel links vorne == Hintergrund ) biege nach links ab;
else if ( Pixel rechts vorne == Hintergrund ) gehe geradeaus; else biege nach rechts ab.
F: Verfolgungsalgorithmus bei 8er Nachbarschaft in Form eines Pseudocodes ?
A: if ( Pixel rechts vorne == Vordergrund ) biege nach rechts ab;
else if ( Pixel links vorne == Vordergrund ) gehe geradeaus; else biege nach links ab.
| F: |  | Gegeben sei ein Grauwertbild in der Form eines 2D-Arrays Byte b[ySize,xSize] und eine Schwelle s und es gilt die 4er Nachbarschaft. Der Verfolgungsalgorithmus befindet sich an der 0-Zelle x,y am Ende eines Ostcracks. Formulieren Sie den nächsten Schritt des Algorithmus. |
A: if ( b[y-1,x] < s ) goto nord;
else if ( b[y,x] < s ) goto ost; else goto sued;
| F: | 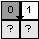 | Gegeben sei ein Grauwertbild in der Form eines 2D-Arrays Byte b[ySize,xSize] und eine Schwelle s und es gilt die 4er Nachbarschaft. Der Verfolgungsalgorithmus befindet sich an der 0-Zelle x,y am Ende eines Südcracks. Formulieren Sie den nächsten Schritt des Algorithmus. |
A: if ( b[y,x] < s ) goto ost;
else if ( b[y,x-1] < s ) goto sued; else goto west;
| F: |  | Gegeben sei ein Grauwertbild in der Form eines 2D-Arrays Byte b[ySize,xSize] und eine Schwelle s und es gilt die 4er Nachbarschaft. Der Verfolgungsalgorithmus befindet sich an der 0-Zelle x,y am Ende eines Westcracks. Formulieren Sie den nächsten Schritt des Algorithmus. |
A: if ( b[y,x-1] < s ) goto sued;
else if ( b[y-1,x-1] < s ) goto west; else goto nord;
| F: |  | Gegeben sei ein Grauwertbild in der Form eines 2D-Arrays Byte b[ySize,xSize] und eine Schwelle s und es gilt die 4er Nachbarschaft. Der Verfolgungsalgorithmus befindet sich an der 0-Zelle x,y am Ende eines Nordcracks. Formulieren Sie den nächsten Schritt des Algorithmus. |
A: if ( b[y-1,x-1] < s ) goto west;
else if ( b[y-1,x] < s ) goto nord; else goto ost;
| F: |  | Gegeben sei ein Grauwertbild in der Form eines 2D-Arrays Byte b[ySize,xSize] und eine Schwelle s und es gilt die 8er Nachbarschaft. Der Verfolgungsalgorithmus befindet sich an der 0-Zelle x,y am Ende eines Ostcracks. Formulieren Sie den nächsten Schritt des Algorithmus. |
A: if ( b[y,x] >= s ) goto sued;
else if ( b[y-1,x] >= s ) goto ost; else goto nord;
| F: |  | Gegeben sei ein Grauwertbild in der Form eines 2D-Arrays Byte b[ySize,xSize] und eine Schwelle s und es gilt die 8er Nachbarschaft. Der Verfolgungsalgorithmus befindet sich an der 0-Zelle x,y am Ende eines Südcracks. Formulieren Sie den nächsten Schritt des Algorithmus. |
A: if ( b[y,x-1] >= s ) goto west;
else if ( b[y,x] >= s ) goto sued; else goto ost;
| F: |  | Gegeben sei ein Grauwertbild in der Form eines 2D-Arrays Byte b[ySize,xSize] und eine Schwelle s und es gilt die 8er Nachbarschaft. Der Verfolgungsalgorithmus befindet sich an der 0-Zelle x,y am Ende eines Westcracks. Formulieren Sie den nächsten Schritt des Algorithmus. |
A: if ( b[y-1,x-1] >= s ) goto nord;
else if ( b[y,x-1] >= s ) goto west; else goto sued;
| F: |  | Gegeben sei ein Grauwertbild in der Form eines 2D-Arrays Byte b[ySize,xSize] und eine Schwelle s und es gilt die 8er Nachbarschaft. Der Verfolgungsalgorithmus befindet sich an der 0-Zelle x,y am Ende eines Nordcracks. Formulieren Sie den nächsten Schritt des Algorithmus. |
A: if ( b[y-1,x] >= s ) goto ost;
else if ( b[y-1,x-1] >= s ) goto nord; else goto west;
F: Wie berechnet man, ausgehend von (x0,y0), die neue Koordinate und die Fläche des Gebiets während der Verfolgung ?
A: Int32 x = x0, y = y0, flaeche = 0;
für alle Richtungen:
{ if ( Richtung == ost ) { x++; flaeche += y; }
else if ( Richtung == sued ) y++;
else if ( Richtung == west ) { x--; flaeche -= y; }
else if ( Richtung == nord ) y--;
}
F: Gegeben sei folgender Chain Code: (1/0)swsseenennww. Zeichnen Sie ein 3x3-Binärbild, das ein Gebiet mit dieser Begrenzung enthält.
A: 011
111
110
F: Gegeben sei eine Gebietsbegrenzung in Form eines Chain Codes. Welche Möglichkeiten gibt es, daraus ein Polygon zu machen ?
A: 1) Jeder Anfangspunkt eines Cracks wird ein Vertex = 1:1 Umwandlung.
2) Vertices werden nur die Anfangspunkte derjenigen Cracks, wo der Code seine Richtung ändert.
3) Approximation durch Geradenstücke mit einem zulässigen Fehler epsilon.
4) Approximation durch Polynome 3. Grades = Bézier-Kurven oder kubische Splines.
F: Approximation durch Geradenstücke mit einem zulässigen Fehler epsilon nach der Gummibandmethode ?
A: 1) Gummiband am aktuellen Point befestigen.
2) Zum nächsten Point gehen, Gummiband streckt sich.
3) Die Abstände aller rückwärtigen Points zum Gummiband berechnen. Ist jeder einzelne Abstand kleiner gleich epsilon, dann weiter bei 2),
4) Fertig, wenn Startpunkt wieder erreicht.
F: Gegeben sei ein Gebiet durch seinen Chain Code (1/0)swsesenennww.
Gesucht: 1:1 Polygon plus dessen Umfang und Fläche.
Ergänzen Sie das folgende Programm an den Stellen, wo ..... steht:
int x0 = 1, y0 = 0; //gegeben
static string cracks = "swsesenennww"; //gegeben
static int x, y, i; //Laufvariable
Point[] p = new Point[cracks.Length+1]; //Platz für geschlossenes Polygon
int perimeter = cracks.Length, area = 0;
p[0].X = x = x0;
p[0].Y = y = y0;
for (i = 1; i <= cracks.Length; i++ )
{ switch( cracks[i-1] )
{ case 'e': ...............................................; break;
case 's': ...............................................; break;
case 'w': ...............................................; break;
case 'n': ...............................................; break;
}
p[i].X = x; p[i].Y = y;
}
A:
{ case 'e': x++; area += y; break;
case 's': y++; break;
case 'w': x--; area -= y; break;
case 'n': y--; break;
}
F: Gegeben sei ein Gebiet durch seinen Chain Code (1,0)swsesenennww.
Gesucht: Schwerpunkt und umschreibendes Rechteck des 1:1 Polygons.
Ergänzen Sie das folgende Programm an den Stellen, wo ..... steht:
int x0 = 1, y0 = 0; //gegeben
static string cracks = "swsesenennww"; //gegeben
int x, y, i; //Laufvariable
int xmin, ymin, xmax, ymax; //umschr. Rechteck
float sx = 0f, sy = 0f; //Schwerpunkt
xmin = xmax = x = x0; //Startwert
ymin = ymax = y = y0; //Startwert
for (i = 0; i < cracks.Length; i++ )
{ switch( cracks[i] )
{ case 'e': ...............................................; break;
case 's': ...............................................; break;
case 'w': ...............................................; break;
case 'n': ...............................................; break;
}
sx += ......; sy += ......;
}
sx /= ......; sy /= ......;
A:
{ case 'e': x++; if ( x > xmax ) xmax++; break;
case 's': y++; if ( y > ymax ) ymax++; break;
case 'w': x--; if ( x < xmin ) xmin--; break;
case 'n': y--; if ( y < ymin ) ymin--; break;
}
sx += x; sy += y;
}
sx /= cracks.Length; sy /= cracks.Length;| top of page: |