Home Content «FogFilter MedianFilter»

Textbook on Image Filters
Chapter 4 - The Gaussian Filter
Copyright: V. Miszalok
Last Modified:
Home Content «FogFilter MedianFilter»

Copyright: V. Miszalok
Last Modified:
The average filter and its variations give an equal vote to all neighbors
around the center of the rectangular filter kernel.
A better idea is to give more power to near neighbors than to distant ones.
A Gaussian distribution clustered around the kernel center is an
intelligent way to distribute graded power to near and distant neighbors.
The declining voting power from center to periphery can be graded between completely flat a = 0.0
(→ average filter) and extremely steep a >> 10 (→ no filtering at all).
//C#-Code of the 5x5 Gaussian kernel program:
double stdDev = stdDevSlider.Value, steepness;
steepness = - 1.0 / ( 2.0 * stdDev * stdDev ); //stdDev != 0
int votes, sum = 0;
for ( int y=-2; y <= 2; y++ )
for ( int x=-2; x <= 2; x++ )
{ votes = Convert.ToInt32( 100 * Math.Exp( steepness*(x*x + y*y) ) );
votesTextBox[y+2,x+2].Text = votes.ToString();
sum += votes;
}
sumTextBox.Text = "Sum of Votes = " + sum.ToString();
The Terms "Kernel" and "Vote":
Kernel k: rectangular window carrying the filter area with
an odd integer kw = kernel width and an odd integer kh = kernel height.
integer kwh = kw/2 = half of kernel width and
integer khh = kh/2 = half of kernel height and
integer -kw <= xx <= kw → horizontally running index and
integer -kh <= yy <= kh → vertically running index.
The adress of the kernel center is [0,0].
The kernel can be empty just marking a neighborhood or
the kernel can be a matrix of relative power values = votes.
Vote: numerical value of a kernel position carrying its relative power compared to the center.
How to use the demo program:
The "Open Image"-button, both large text boxes and the three sliders are self-explaining.
But underneath the lowest slider appear a tiny gray-value image and a lowest vote" text box.
The tiny gray-value image size changes when you drag the FilterWidth- and/or the FilterHeight-slider.
Its size grows and shrinks proportional to the filter size.
The Std.Dev.-slider influences the size of the displayed white spot.
Std.Dev. = 0.0 produces just one white pixel centrally while Std.Dev. = 158 fills the image completely with white pixels.
Let's call it the kernel image because it shows the ground-plan of the 2D-Gaussian bell in the limits of the filter size.
A white pixel denotes a voting power of 100% and a black pixel denotes 0% which means no vote at all.
The lowest vote" text box displays the value of the pixel in the upper left corner of the kernel image.
No other pixel is farer away from the center.
When its vote is 0, the filter size is unnecessarily big compared with the Std.Dev.
When its vote is >> 1, the filter is too small to contain the bell.
Caution: It makes little sense to choose a big filter size together with a small standard deviation.
or to choose a big standard deviation together with a small filter.
The demo program doesn't prevent you from such nonsense.
In order not to confuse their customers, commercial fast Gaussian filters let you choose either the filter size or the standard deviation.
In the first case they compute a standard deviation fitting to the filter size with a lowest vote of 1.
In the second case they compute a quadratic filter fitting to the bell so that its lowest vote comes out to be about 1 again.
Experiments:
Drag the Std.Dev. slider between 0.00 and 158.
Observe the small image underneath the Std.Dev. slider and the "lowest vote" textbox.
A low standard deviation produces a black image with a white spot,
but high standard deviations produce a almost white image.
A standard deviation of 0 doesn't filter at all regardless of the filter size.
A filter size of 1x1 doesn't filter at all regardless of the standard deviation.
A result of filtering with standard deviations with lowest votes > 90 is almost identical with average filtering.
With standard deviations < 1.0 nothing changes when the filter size increases > 5.
Unfortunately the Gaussian filter is slow because it needs N2 multiplications and additions per pixel (N being the size of a quadratic kernel).
 |
Prof. Vladimir Kovalevsky published the following idea of a recursive filter to fasten it: The Fast Gaussian Filter.
|
Guidance:
At first you just see a vertical white bar in the middle of the black canvas.
This white bar in the mid of an 1D-array of (invisible) black bars visualizes a perfectly focused optical spot.
Click the Button "Average Filter !" to start and whenever you have changed one of the 3 sliders.
There are 4 resulting drawings:
A set of symmetrically distributed gray columns showing the effect of repeated average filtering.
A red hull curve that connects the top center points of all columns.
A green hull curve that represents the best fitting Gaussian bell curve.
A text box on the left with a green figure showing the standard deviation.
Three sliders enable the setting of three parameters:
The Columns slider: Chooses the length of the 1D pixel array. Each single column narrows when the array grows.
The Filter Width slider: Chooses the kernel size of the 1D average filter.
The Repetitions slider: Chooses the no of repetitions of the average filter.
Experiments:
Drag the Columns slider between 13 and 101 and click "Average Filter !".
It just stretches the canvas horizontally but doesn't change the final StdDev figure.
A small StdDev can better be observed with a few fat columns whereas big ones need a long array.
Set Columns to 101 and drag the Filter Width slider between 3 and 49 and notice the growing filter effect.
Set Columns to 101 and drag the Repetitions slider between 3 and 25 and notice the growing filter effect.
Notice that the Fast Gaussian Filter just realizes some specific StdDevs with unreachable StdDevs between.
Notice that large StdDevs can be realized with big Filter Width or with high Repetitions (or both).
Notice that 3 Repetitions are enough for good bell curve approximations.
Heavy blurring can be achieved by a big average filter and/or many repetitions.
Using the fast average filter, big filter sizes take the same time as small ones but many repetitions heavily matter.
Furthermore the border problem occurs at any repetition. Each shrinks the averaged result by half of the average filter size.
For sake of velocity and narrow borders we therefore restrict the repetition rate to 3.
This restricts us to just a few standard deviations: 1.6, 2.7, 3.8 etc.
Guidance:
1. Drag the Quadratic Filter Width slider.
2. Open more JPG or PNG images.
Experiments:
Drag the Quadratic Filter Width slider between 3 and 31 and notice:
Blurring depends on the average filter size.
The size of the Equivalent Gaussian Kernel depends on the average filter size.
The Equivalent Gaussian Kernel standard deviation depends on the average filter size.
The fast Gaussian filter is about 5-10 times faster than the equivalent simple filter.
Filtering time depends on the image size but not on the average filter size.
Border problem:
The fast Gaussian filter has a big border problem that the simple filter hasn't.
The thickness of the black borders is triple of the average filter half size.
e.g. The 31*31 filter has a border thickness of 15+15+15 = 45.
Solutions of the border problem:
Fast solution: Same fill by copy as with the fast average filter (see; Average Filter).
Slow solution: Additional simple Gaussian filtering of the border areas after fast filtering.
Q: What is a Gaussian Filter ?
A:
It mimics an optical point spread function by giving near neighbors more influence than distant ones.
Its weight values are Gauss-distributed in
rotational symmetry around the center of a rectangular kernel:
votes = maxVote*e-d*d/(2*sigma*sigma).
where d = distance from the center pixel and sigma = selected standard deviation.
votes are relative weights in percent and maxVote=100%.
Q: How to design a Gaussian filter kernel ?
A:
Choose a reasonable standard deviation sigma.
Choose a quadratic filter kernel size so that even the most distant neighbors will obtain a small amount of votes.
Choose the no of votes of the center of the kernel = maxVote: e,g.: 1.0 or 100 or 255.
For each neighbor(xx,yy) abround the kernel center(x,y):
dx=x-xx; dy=y-yy; d(x,y)=SquareRoot(dx*dx+dy*dy)..
dd = d(x,y)*d(x,y); ss = sigma*sigma;
vote(x,y) = maxVote* e-dd/(2*ss)
Q: What is the fast Gaussian filter ? Disadvantages compared to the slow Gaussian filter ?
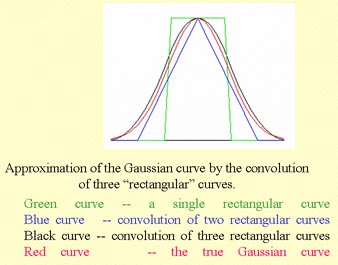
A: Repeating the fast average filter 3 times produces nearly the same blurring as a Gaussian filter does,
but is 5-10 times faster.
Disadvantages:
Any fast gauss filter just has one fixed standard deviation depending on its filter size and repetition rate.
Thick black borders remain unfiltered and must be post-processed.
Q: Usual fast Gaussian filters just use three repetitions of the fast average filter. Why ?
A; Heavy blurring can be achieved by many repetitions of a small filter or by few repetitions of a big filter.
More repetitions take more time but an increased filter size doesn't.
Consequence: It saves time to increase filter size instead of the repetition rate.